Black Hole Spectra¶
Black hole spectra can be generated by combining a BlackHoles (for particle, BlackHole for parametric) object with an EmissionModel, translating the physical properties of the blackhole(s) (e.g. mass, accretion_rate, etc.) to a spectral energy distribution.
These models are described in detail in the emission model docs. Here, we’ll use an instance of a UnifiedAGN model for demonstration purposes.
The following sections demonstrate the generation of combined spectra (which is the same for both parametric and particle BlackHoles) and per-particle spectra.
[1]:
import numpy as np
from unyt import K, Mpc, Msun, cm, deg, yr
from synthesizer import Grid
from synthesizer.emission_models import (
Greybody,
UnifiedAGN,
)
from synthesizer.emission_models.attenuation import PowerLaw
from synthesizer.parametric import BlackHole
# Get the NLR and BLR grids
nlr_grid = Grid("test_grid_agn-nlr")
blr_grid = Grid("test_grid_agn-blr")
# Initialise the BlackHole object setting most of the key attributes
blackhole = BlackHole(
mass=1e8 * Msun,
inclination=60 * deg,
accretion_rate_eddington=0.1,
covering_fraction_nlr=0.1,
covering_fraction_blr=0.1,
metallicity=0.01,
theta_torus=20 * deg,
)
# Initialise the UnifiedAGN model
uniagn = UnifiedAGN(
nlr_grid,
blr_grid,
ionisation_parameter_nlr=0.01,
hydrogen_density_nlr=1e4 * cm**-3,
ionisation_parameter_blr=0.1,
hydrogen_density_blr=1e10 * cm**-3,
torus_emission_model=Greybody(1000 * K, 1.5),
)
Integrated spectra¶
To generate integrated spectra we simply call the component’s get_spectra method. This method will populate the component’s spectra attribute with a dictionary containing Sed objects for each spectra in the EmissionModel. It will also return the spectra at the root of the EmissionModel.
[2]:
# Get the spectra using a unified agn model (instantiated elsewhere)
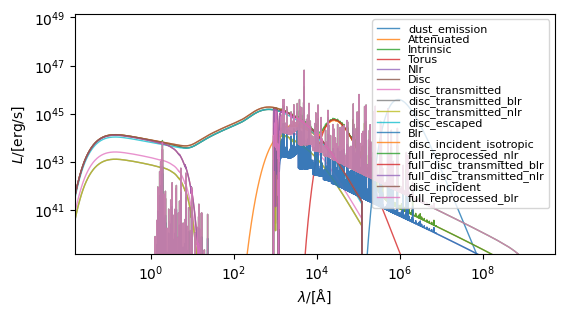
spectra = blackhole.get_spectra(uniagn)
fig, ax = blackhole.plot_spectra(
show=True,
ylimits=(10**27.5, 10**34.0),
figsize=(10, 8),
)
print(blackhole.model_param_cache)
{'disc_incident_masked': {'inclination': unyt_array(60, 'degree'), 'theta_torus': unyt_quantity(20, 'degree'), 'torus_edgeon_cond': np.int64(80), 'mass': unyt_array(1.e+08, 'Msun'), 'masses': unyt_array(1.e+08, 'Msun'), 'log10masses': array(8.), 'accretion_rate_eddington': np.float64(0.1), 'accretion_rates_eddington': np.float64(0.1), 'log10accretion_rates_eddington': np.float64(-1.0), 'cosine_inclination': np.float64(0.5000000000000001), 'cosine_inclinations': np.float64(0.5000000000000001), 'metallicity': 0.01, 'metallicities': 0.01, 'ionisation_parameter': 0.1, 'ionisation_parameters': 0.1, 'hydrogen_density': unyt_quantity(1.e+09, 'cm**(-3)'), 'hydrogen_densities': unyt_quantity(1.e+09, 'cm**(-3)'), 'bolometric_luminosity': unyt_array(3.284e+11, 'Lsun'), 'bolometric_luminosities': array(3.284e+11), 'extract': 'incident', 'emitter': 'blackhole', 'masks': 'torus_edgeon_cond < 90 degree'}, 'disc_transmitted_nlr_full': {'inclination': unyt_array(60, 'degree'), 'theta_torus': unyt_quantity(20, 'degree'), 'torus_edgeon_cond': np.int64(80), 'log10masses': array(8.), 'log10accretion_rates_eddington': np.float64(-1.0), 'cosine_inclination': np.float64(0.5000000000000001), 'cosine_inclinations': np.float64(0.5000000000000001), 'metallicity': 0.01, 'metallicities': 0.01, 'ionisation_parameter': 0.01, 'ionisation_parameters': 0.01, 'hydrogen_density': unyt_quantity(10000., 'cm**(-3)'), 'hydrogen_densities': unyt_quantity(10000., 'cm**(-3)'), 'bolometric_luminosity': unyt_array(3.284e+11, 'Lsun'), 'bolometric_luminosities': array(3.284e+11), 'extract': 'transmitted', 'emitter': 'blackhole', 'masks': 'torus_edgeon_cond < 90 degree'}, 'disc_transmitted_blr_full': {'inclination': unyt_array(60, 'degree'), 'theta_torus': unyt_quantity(20, 'degree'), 'torus_edgeon_cond': np.int64(80), 'log10masses': array(8.), 'log10accretion_rates_eddington': np.float64(-1.0), 'cosine_inclination': np.float64(0.5000000000000001), 'cosine_inclinations': np.float64(0.5000000000000001), 'metallicity': 0.01, 'metallicities': 0.01, 'ionisation_parameter': 0.1, 'ionisation_parameters': 0.1, 'hydrogen_density': unyt_quantity(1.e+09, 'cm**(-3)'), 'hydrogen_densities': unyt_quantity(1.e+09, 'cm**(-3)'), 'bolometric_luminosity': unyt_array(3.284e+11, 'Lsun'), 'bolometric_luminosities': array(3.284e+11), 'extract': 'transmitted', 'emitter': 'blackhole', 'masks': 'torus_edgeon_cond < 90 degree'}, 'full_reprocessed_nlr': {'log10masses': array(8.), 'log10accretion_rates_eddington': np.float64(-1.0), 'cosine_inclination': 0.5, 'cosine_inclinations': 0.5, 'metallicity': 0.01, 'metallicities': 0.01, 'ionisation_parameter': 0.01, 'ionisation_parameters': 0.01, 'hydrogen_density': unyt_quantity(10000., 'cm**(-3)'), 'hydrogen_densities': unyt_quantity(10000., 'cm**(-3)'), 'bolometric_luminosity': unyt_array(3.284e+11, 'Lsun'), 'bolometric_luminosities': array(3.284e+11), 'extract': 'nebular', 'emitter': 'blackhole'}, 'full_reprocessed_blr': {'inclination': unyt_array(60, 'degree'), 'theta_torus': unyt_quantity(20, 'degree'), 'torus_edgeon_cond': np.int64(80), 'log10masses': array(8.), 'log10accretion_rates_eddington': np.float64(-1.0), 'cosine_inclination': 0.5, 'cosine_inclinations': 0.5, 'metallicity': 0.01, 'metallicities': 0.01, 'ionisation_parameter': 0.1, 'ionisation_parameters': 0.1, 'hydrogen_density': unyt_quantity(1.e+09, 'cm**(-3)'), 'hydrogen_densities': unyt_quantity(1.e+09, 'cm**(-3)'), 'bolometric_luminosity': unyt_array(3.284e+11, 'Lsun'), 'bolometric_luminosities': array(3.284e+11), 'extract': 'nebular', 'emitter': 'blackhole', 'masks': 'torus_edgeon_cond < 90 degree'}, 'disc_incident_isotropic': {'log10masses': array(8.), 'log10accretion_rates_eddington': np.float64(-1.0), 'cosine_inclination': 0.5, 'cosine_inclinations': 0.5, 'metallicity': 0.01, 'metallicities': 0.01, 'ionisation_parameter': 0.1, 'ionisation_parameters': 0.1, 'hydrogen_density': unyt_quantity(1.e+09, 'cm**(-3)'), 'hydrogen_densities': unyt_quantity(1.e+09, 'cm**(-3)'), 'bolometric_luminosity': unyt_array(3.284e+11, 'Lsun'), 'bolometric_luminosities': array(3.284e+11), 'extract': 'incident', 'emitter': 'blackhole'}, 'disc_transmitted_nlr_isotropic_full': {'log10masses': array(8.), 'log10accretion_rates_eddington': np.float64(-1.0), 'cosine_inclination': 0.5, 'cosine_inclinations': 0.5, 'metallicity': 0.01, 'metallicities': 0.01, 'ionisation_parameter': 0.01, 'ionisation_parameters': 0.01, 'hydrogen_density': unyt_quantity(10000., 'cm**(-3)'), 'hydrogen_densities': unyt_quantity(10000., 'cm**(-3)'), 'bolometric_luminosity': unyt_array(3.284e+11, 'Lsun'), 'bolometric_luminosities': array(3.284e+11), 'extract': 'transmitted', 'emitter': 'blackhole'}, 'disc_transmitted_blr_isotropic_full': {'log10masses': array(8.), 'log10accretion_rates_eddington': np.float64(-1.0), 'cosine_inclination': 0.5, 'cosine_inclinations': 0.5, 'metallicity': 0.01, 'metallicities': 0.01, 'ionisation_parameter': 0.1, 'ionisation_parameters': 0.1, 'hydrogen_density': unyt_quantity(1.e+09, 'cm**(-3)'), 'hydrogen_densities': unyt_quantity(1.e+09, 'cm**(-3)'), 'bolometric_luminosity': unyt_array(3.284e+11, 'Lsun'), 'bolometric_luminosities': array(3.284e+11), 'extract': 'transmitted', 'emitter': 'blackhole'}, 'full_continuum_nlr': {'log10masses': array(8.), 'log10accretion_rates_eddington': np.float64(-1.0), 'cosine_inclination': 0.5, 'cosine_inclinations': 0.5, 'metallicity': 0.01, 'metallicities': 0.01, 'ionisation_parameter': 0.01, 'ionisation_parameters': 0.01, 'hydrogen_density': unyt_quantity(10000., 'cm**(-3)'), 'hydrogen_densities': unyt_quantity(10000., 'cm**(-3)'), 'bolometric_luminosity': unyt_array(3.284e+11, 'Lsun'), 'bolometric_luminosities': array(3.284e+11), 'extract': 'nebular_continuum', 'emitter': 'blackhole'}, 'disc_incident': {'log10masses': array(8.), 'log10accretion_rates_eddington': np.float64(-1.0), 'cosine_inclination': np.float64(0.5000000000000001), 'cosine_inclinations': np.float64(0.5000000000000001), 'metallicity': 0.01, 'metallicities': 0.01, 'ionisation_parameter': 0.1, 'ionisation_parameters': 0.1, 'hydrogen_density': unyt_quantity(1.e+09, 'cm**(-3)'), 'hydrogen_densities': unyt_quantity(1.e+09, 'cm**(-3)'), 'bolometric_luminosity': unyt_array(3.284e+11, 'Lsun'), 'bolometric_luminosities': array(3.284e+11), 'extract': 'incident', 'emitter': 'blackhole'}, 'full_continuum_blr': {'inclination': unyt_array(60, 'degree'), 'theta_torus': unyt_quantity(20, 'degree'), 'torus_edgeon_cond': np.int64(80), 'log10masses': array(8.), 'log10accretion_rates_eddington': np.float64(-1.0), 'cosine_inclination': 0.5, 'cosine_inclinations': 0.5, 'metallicity': 0.01, 'metallicities': 0.01, 'ionisation_parameter': 0.1, 'ionisation_parameters': 0.1, 'hydrogen_density': unyt_quantity(1.e+09, 'cm**(-3)'), 'hydrogen_densities': unyt_quantity(1.e+09, 'cm**(-3)'), 'bolometric_luminosity': unyt_array(3.284e+11, 'Lsun'), 'bolometric_luminosities': array(3.284e+11), 'extract': 'nebular_continuum', 'emitter': 'blackhole', 'masks': 'torus_edgeon_cond < 90 degree'}, 'disc_escaped': {'transmission_fraction_escape': 0.8, 'apply_to': 'disc_incident_masked', 'transformer': "CoveringFraction(covering_attrs=('transmission_fraction_escape',))", 'emitter': 'blackhole'}, 'disc_transmitted_nlr': {'transmission_fraction_nlr': 0.1, 'apply_to': 'disc_transmitted_nlr_full', 'transformer': "CoveringFraction(covering_attrs=('transmission_fraction_nlr',))", 'emitter': 'blackhole'}, 'disc_transmitted_blr': {'transmission_fraction_blr': 0.1, 'apply_to': 'disc_transmitted_blr_full', 'transformer': "CoveringFraction(covering_attrs=('transmission_fraction_blr',))", 'emitter': 'blackhole'}, 'nlr': {'covering_fraction_nlr': 0.1, 'apply_to': 'full_reprocessed_nlr', 'transformer': "CoveringFraction(covering_attrs=('covering_fraction_nlr',))", 'emitter': 'blackhole'}, 'blr': {'covering_fraction_blr': 0.1, 'apply_to': 'full_reprocessed_blr', 'transformer': "CoveringFraction(covering_attrs=('covering_fraction_blr',))", 'emitter': 'blackhole'}, 'torus': {'temperature': unyt_quantity(1000, 'K'), 'emissivity': 1.5, 'generator': 'Greybody(scaler=disc_incident_isotropic, temperature=1000 K, emissivity=1.5, optically_thin=True, lam_0=100.0 μm)', 'emitter': 'blackhole'}, 'disc_escaped_isotropic': {'covering_fraction_blr': 0.1, 'covering_fraction_nlr': 0.1, 'apply_to': 'disc_incident_isotropic', 'transformer': "EscapingFraction(covering_attrs=('covering_fraction_blr', 'covering_fraction_nlr'))", 'emitter': 'blackhole'}, 'disc_transmitted_nlr_isotropic': {'covering_fraction_nlr': 0.1, 'apply_to': 'disc_transmitted_nlr_isotropic_full', 'transformer': "CoveringFraction(covering_attrs=('covering_fraction_nlr',))", 'emitter': 'blackhole'}, 'disc_transmitted_blr_isotropic': {'covering_fraction_blr': 0.1, 'apply_to': 'disc_transmitted_blr_isotropic_full', 'transformer': "CoveringFraction(covering_attrs=('covering_fraction_blr',))", 'emitter': 'blackhole'}, 'nlr_continuum': {'covering_fraction_nlr': 0.1, 'apply_to': 'full_continuum_nlr', 'transformer': "CoveringFraction(covering_attrs=('covering_fraction_nlr',))", 'emitter': 'blackhole'}, 'blr_continuum': {'covering_fraction_blr': 0.1, 'apply_to': 'full_continuum_blr', 'transformer': "CoveringFraction(covering_attrs=('covering_fraction_blr',))", 'emitter': 'blackhole'}, 'disc_transmitted_weighted_combination': {'combine': ['disc_escaped', 'disc_transmitted_nlr', 'disc_transmitted_blr'], 'emitter': 'blackhole'}, 'line_regions': {'combine': ['nlr', 'blr'], 'emitter': 'blackhole'}, 'disc_averaged_without_torus': {'combine': ['disc_escaped_isotropic', 'disc_transmitted_nlr_isotropic', 'disc_transmitted_blr_isotropic'], 'emitter': 'blackhole'}, 'disc_transmitted': {'combine': ['disc_transmitted_weighted_combination'], 'emitter': 'blackhole'}, 'disc_averaged': {'torus_fraction': array(0.22222222), 'apply_to': 'disc_averaged_without_torus', 'transformer': "EscapingFraction(covering_attrs=('torus_fraction',))", 'emitter': 'blackhole'}, 'disc': {'combine': ['disc_transmitted'], 'emitter': 'blackhole'}, 'intrinsic': {'combine': ['disc', 'nlr', 'blr', 'torus'], 'emitter': 'blackhole'}}
Including dust attenuation¶
We can also generate spectra including attenuation and emission from diffuse dust along the line of sight to the black hole. This is now possible directly with the UnifiedAGN by passing a dust curve. The optical depth (tau_v) must be available on the emitter (the blackhole) or set by the emission model.
[3]:
tau_v = 0.5
# Initialise the UnifiedAGN model
uniagn_attenuated = UnifiedAGN(
nlr_grid,
blr_grid,
ionisation_parameter_nlr=0.01,
hydrogen_density_nlr=1e4 * cm**-3,
ionisation_parameter_blr=0.1,
hydrogen_density_blr=1e10 * cm**-3,
torus_emission_model=Greybody(1000 * K, 1.5),
diffuse_dust_curve=PowerLaw(slope=-1.0),
tau_v=tau_v,
)
We then follow the same process of calling get_spectra with the new model. The plot here shows luminosity rather than spectral energy density.
[4]:
spectra = blackhole.get_spectra(uniagn_attenuated)
fig, ax = blackhole.plot_spectra(
quantity_to_plot="luminosity",
figsize=(6, 4),
spectra_to_plot=["intrinsic", "attenuated"],
)
The spectra returned by get_spectra is the “dust_emission” spectra at the root of the emission model.
[5]:
print(spectra)
+----------------------------------------------------------------------------------------------------+
| SED |
+---------------------------+------------------------------------------------------------------------+
| Attribute | Value |
+---------------------------+------------------------------------------------------------------------+
| redshift | 0 |
+---------------------------+------------------------------------------------------------------------+
| vel_shifted | False |
+---------------------------+------------------------------------------------------------------------+
| ndim | 1 |
+---------------------------+------------------------------------------------------------------------+
| nlam | 9244 |
+---------------------------+------------------------------------------------------------------------+
| shape | (9244,) |
+---------------------------+------------------------------------------------------------------------+
| lam (9244,) | 1.30e-04 Å -> 2.99e+11 Å (Mean: 9.73e+09 Å) |
+---------------------------+------------------------------------------------------------------------+
| lnu (9244,) | 0.00e+00 erg/(Hz*s) -> 1.07e+31 erg/(Hz*s) (Mean: 1.12e+29 erg/(Hz*s)) |
+---------------------------+------------------------------------------------------------------------+
| bolometric_luminosity | 118441669615.35707 Lsun |
+---------------------------+------------------------------------------------------------------------+
| nu (9244,) | 1.00e+07 Hz -> 2.31e+22 Hz (Mean: 8.51e+19 Hz) |
+---------------------------+------------------------------------------------------------------------+
| energy (9244,) | 4.14e-08 eV -> 9.56e+07 eV (Mean: 3.52e+05 eV) |
+---------------------------+------------------------------------------------------------------------+
| frequency (9244,) | 1.00e+07 Hz -> 2.31e+22 Hz (Mean: 8.51e+19 Hz) |
+---------------------------+------------------------------------------------------------------------+
| llam (9244,) | 0.00e+00 Lsun/Å -> 6.17e+07 Lsun/Å (Mean: 6.89e+05 Lsun/Å) |
+---------------------------+------------------------------------------------------------------------+
| luminosity (9244,) | 0.00e+00 Lsun -> 3.09e+11 Lsun (Mean: 3.84e+09 Lsun) |
+---------------------------+------------------------------------------------------------------------+
| luminosity_lambda (9244,) | 0.00e+00 Lsun/Å -> 6.17e+07 Lsun/Å (Mean: 6.89e+05 Lsun/Å) |
+---------------------------+------------------------------------------------------------------------+
| luminosity_nu (9244,) | 0.00e+00 erg/(Hz*s) -> 1.07e+31 erg/(Hz*s) (Mean: 1.12e+29 erg/(Hz*s)) |
+---------------------------+------------------------------------------------------------------------+
| wavelength (9244,) | 1.30e-04 Å -> 2.99e+11 Å (Mean: 9.73e+09 Å) |
+---------------------------+------------------------------------------------------------------------+
However, all the spectra are stored within a dictionary under the spectra attribute.
[6]:
print(blackhole.spectra)
{'disc_incident_masked': <synthesizer.emissions.sed.Sed object at 0x7efcc8f11420>, 'disc_transmitted_nlr_full': <synthesizer.emissions.sed.Sed object at 0x7efcc8f123b0>, 'disc_transmitted_blr_full': <synthesizer.emissions.sed.Sed object at 0x7efcc8f11570>, 'full_reprocessed_nlr': <synthesizer.emissions.sed.Sed object at 0x7efc7bbb1f30>, 'full_reprocessed_blr': <synthesizer.emissions.sed.Sed object at 0x7efc7d6705b0>, 'disc_incident_isotropic': <synthesizer.emissions.sed.Sed object at 0x7efc7bbb1db0>, 'disc_transmitted_nlr_isotropic_full': <synthesizer.emissions.sed.Sed object at 0x7efc7bbb0c40>, 'disc_transmitted_blr_isotropic_full': <synthesizer.emissions.sed.Sed object at 0x7efc7bbb1000>, 'full_continuum_nlr': <synthesizer.emissions.sed.Sed object at 0x7efc7d670670>, 'disc_incident': <synthesizer.emissions.sed.Sed object at 0x7efc7be98520>, 'full_continuum_blr': <synthesizer.emissions.sed.Sed object at 0x7efc7d6707c0>, 'disc_escaped': <synthesizer.emissions.sed.Sed object at 0x7efc7bbb2080>, 'disc_transmitted_nlr': <synthesizer.emissions.sed.Sed object at 0x7efc7bbb2200>, 'disc_transmitted_blr': <synthesizer.emissions.sed.Sed object at 0x7efcd0199a50>, 'nlr': <synthesizer.emissions.sed.Sed object at 0x7efc7bbb1b40>, 'blr': <synthesizer.emissions.sed.Sed object at 0x7efc7bbb21a0>, 'torus': <synthesizer.emissions.sed.Sed object at 0x7efc7d670340>, 'disc_escaped_isotropic': <synthesizer.emissions.sed.Sed object at 0x7efc7bb5f8e0>, 'disc_transmitted_nlr_isotropic': <synthesizer.emissions.sed.Sed object at 0x7efc7bbb0580>, 'disc_transmitted_blr_isotropic': <synthesizer.emissions.sed.Sed object at 0x7efc7bbb20e0>, 'nlr_continuum': <synthesizer.emissions.sed.Sed object at 0x7efc7bbb0b20>, 'blr_continuum': <synthesizer.emissions.sed.Sed object at 0x7efc7bbb2140>, 'disc_transmitted_weighted_combination': <synthesizer.emissions.sed.Sed object at 0x7efc7bbb1c90>, 'line_regions': <synthesizer.emissions.sed.Sed object at 0x7efc7bbb1c60>, 'disc_averaged_without_torus': <synthesizer.emissions.sed.Sed object at 0x7efc7bbb1e10>, 'disc_transmitted': <synthesizer.emissions.sed.Sed object at 0x7efc7bbb1cc0>, 'disc_averaged': <synthesizer.emissions.sed.Sed object at 0x7efc7bbb2170>, 'disc': <synthesizer.emissions.sed.Sed object at 0x7efc7bbb1f00>, 'intrinsic': <synthesizer.emissions.sed.Sed object at 0x7efc7bbb1c30>, 'attenuated': <synthesizer.emissions.sed.Sed object at 0x7efc7bb5fd00>}
Particle spectra¶
To demonstrate the particle spectra functionality we first generate some mock particle black hole data, and initialise a BlackHoles object.
[7]:
from synthesizer.particle import BlackHoles
# Make fake properties
n = 4
masses = 10 ** np.random.uniform(low=7, high=9, size=n) * Msun
coordinates = np.random.normal(0, 1.5, (n, 3)) * Mpc
accretion_rates = 10 ** np.random.uniform(low=-2, high=1, size=n) * Msun / yr
metallicities = np.full(n, 0.01)
# And get the black holes object
blackholes = BlackHoles(
masses=masses,
coordinates=coordinates,
accretion_rates=accretion_rates,
metallicities=metallicities,
ionisation_parameter_nlr=0.01,
hydrogen_density_nlr=1e4 * cm**-3,
ionisation_parameter_blr=0.1,
hydrogen_density_blr=1e10 * cm**-3,
)
To generate a spectra for each black hole (per particle) we use the same emission model, but we need to tell the model to produce a spectrum for each particle. This is done by setting the per_particle flag to True on the model.
[8]:
uniagn_attenuated.set_per_particle(True)
With that done we just call the same get_spectra method on the component, and the particle spectra will be stored in the particle_spectra attribute of the component.
[9]:
spectra = blackholes.get_spectra(uniagn_attenuated, verbose=True)
Again, the returned spectra is the “dust_emission” spectra from the root of the model.
[10]:
print(spectra)
+------------------------------------------------------------------------------------------------------+
| SED |
+-----------------------------+------------------------------------------------------------------------+
| Attribute | Value |
+-----------------------------+------------------------------------------------------------------------+
| redshift | 0 |
+-----------------------------+------------------------------------------------------------------------+
| vel_shifted | False |
+-----------------------------+------------------------------------------------------------------------+
| ndim | 2 |
+-----------------------------+------------------------------------------------------------------------+
| nlam | 9244 |
+-----------------------------+------------------------------------------------------------------------+
| shape | (4, 9244) |
+-----------------------------+------------------------------------------------------------------------+
| lam (9244,) | 1.30e-04 Å -> 2.99e+11 Å (Mean: 9.73e+09 Å) |
+-----------------------------+------------------------------------------------------------------------+
| lnu (4, 9244) | 0.00e+00 erg/(Hz*s) -> 2.37e+32 erg/(Hz*s) (Mean: 6.61e+29 erg/(Hz*s)) |
+-----------------------------+------------------------------------------------------------------------+
| bolometric_luminosity (4,) | 5.40e+09 Lsun -> 3.07e+12 Lsun (Mean: 8.41e+11 Lsun) |
+-----------------------------+------------------------------------------------------------------------+
| nu (9244,) | 1.00e+07 Hz -> 2.31e+22 Hz (Mean: 8.51e+19 Hz) |
+-----------------------------+------------------------------------------------------------------------+
| energy (9244,) | 4.14e-08 eV -> 9.56e+07 eV (Mean: 3.52e+05 eV) |
+-----------------------------+------------------------------------------------------------------------+
| frequency (9244,) | 1.00e+07 Hz -> 2.31e+22 Hz (Mean: 8.51e+19 Hz) |
+-----------------------------+------------------------------------------------------------------------+
| llam (4, 9244) | 0.00e+00 Lsun/Å -> 1.36e+09 Lsun/Å (Mean: 5.93e+06 Lsun/Å) |
+-----------------------------+------------------------------------------------------------------------+
| luminosity (4, 9244) | 0.00e+00 Lsun -> 6.82e+12 Lsun (Mean: 2.73e+10 Lsun) |
+-----------------------------+------------------------------------------------------------------------+
| luminosity_lambda (4, 9244) | 0.00e+00 Lsun/Å -> 1.36e+09 Lsun/Å (Mean: 5.93e+06 Lsun/Å) |
+-----------------------------+------------------------------------------------------------------------+
| luminosity_nu (4, 9244) | 0.00e+00 erg/(Hz*s) -> 2.37e+32 erg/(Hz*s) (Mean: 6.61e+29 erg/(Hz*s)) |
+-----------------------------+------------------------------------------------------------------------+
| wavelength (9244,) | 1.30e-04 Å -> 2.99e+11 Å (Mean: 9.73e+09 Å) |
+-----------------------------+------------------------------------------------------------------------+
While the spectra produced by get_particle_spectra are stored in a dictionary under the particle_spectra attribute.
[11]:
print(blackholes.particle_spectra)
{'disc_incident_masked': <synthesizer.emissions.sed.Sed object at 0x7efc78aa7490>, 'disc_transmitted_nlr_full': <synthesizer.emissions.sed.Sed object at 0x7efc78aa73d0>, 'disc_transmitted_blr_full': <synthesizer.emissions.sed.Sed object at 0x7efc78aa6800>, 'full_reprocessed_nlr': <synthesizer.emissions.sed.Sed object at 0x7efc7be985e0>, 'full_reprocessed_blr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa7700>, 'disc_incident_isotropic': <synthesizer.emissions.sed.Sed object at 0x7efc78aa7760>, 'full_continuum_blr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa6470>, 'disc_transmitted_nlr_isotropic_full': <synthesizer.emissions.sed.Sed object at 0x7efc78aa4c10>, 'disc_transmitted_blr_isotropic_full': <synthesizer.emissions.sed.Sed object at 0x7efcd0199810>, 'disc_incident': <synthesizer.emissions.sed.Sed object at 0x7efc78aa7430>, 'full_continuum_nlr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa6890>, 'disc_escaped': <synthesizer.emissions.sed.Sed object at 0x7efc78aa5cc0>, 'disc_transmitted_nlr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa7730>, 'disc_transmitted_blr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa64a0>, 'nlr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa6e60>, 'blr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa7670>, 'torus': <synthesizer.emissions.sed.Sed object at 0x7efc78aa5e10>, 'disc_escaped_isotropic': <synthesizer.emissions.sed.Sed object at 0x7efc78aa6980>, 'blr_continuum': <synthesizer.emissions.sed.Sed object at 0x7efc78aa6b30>, 'disc_transmitted_nlr_isotropic': <synthesizer.emissions.sed.Sed object at 0x7efc78aa6e90>, 'disc_transmitted_blr_isotropic': <synthesizer.emissions.sed.Sed object at 0x7efc78aa6920>, 'nlr_continuum': <synthesizer.emissions.sed.Sed object at 0x7efc78aa5ed0>, 'disc_transmitted_weighted_combination': <synthesizer.emissions.sed.Sed object at 0x7efc78a673d0>, 'line_regions': <synthesizer.emissions.sed.Sed object at 0x7efc78a67940>, 'disc_averaged_without_torus': <synthesizer.emissions.sed.Sed object at 0x7efc78a676d0>, 'disc_transmitted': <synthesizer.emissions.sed.Sed object at 0x7efc78a67970>, 'disc_averaged': <synthesizer.emissions.sed.Sed object at 0x7efc78a67580>, 'disc': <synthesizer.emissions.sed.Sed object at 0x7efc78a67eb0>, 'intrinsic': <synthesizer.emissions.sed.Sed object at 0x7efc788d1de0>, 'attenuated': <synthesizer.emissions.sed.Sed object at 0x7efc78a67b20>}
Integrating spectra¶
The integrated spectra are automatically produced alongside per particle spectra. However, if we wanted to explictly get the integrated spectra from the particle spectra we just generated (for instance if we had made some modification after generation), we can call the integrate_particle_spectra method. This method will sum the individual spectra and populate the spectra dictionary.
Note, we can also integrate individual spectra using the Sed.sum() method.
[12]:
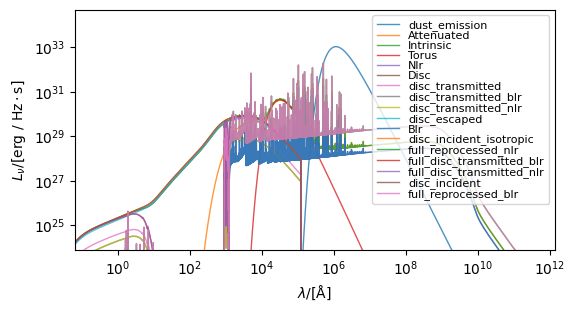
print(blackholes.spectra)
blackholes.integrate_particle_spectra()
print(blackholes.spectra)
fig, ax = blackholes.plot_spectra(
show=True, ylimits=(10**28.5, 10**34.0), figsize=(9, 7.2)
)
{'disc_incident_masked': <synthesizer.emissions.sed.Sed object at 0x7efc78aa40d0>, 'disc_transmitted_nlr_full': <synthesizer.emissions.sed.Sed object at 0x7efc78aa4790>, 'disc_transmitted_blr_full': <synthesizer.emissions.sed.Sed object at 0x7efc78aa64d0>, 'full_reprocessed_nlr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa6fe0>, 'full_reprocessed_blr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa4c70>, 'disc_incident_isotropic': <synthesizer.emissions.sed.Sed object at 0x7efc78aa5fc0>, 'full_continuum_blr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa6200>, 'disc_transmitted_nlr_isotropic_full': <synthesizer.emissions.sed.Sed object at 0x7efc78aa5240>, 'disc_transmitted_blr_isotropic_full': <synthesizer.emissions.sed.Sed object at 0x7efc7bb5ffa0>, 'disc_incident': <synthesizer.emissions.sed.Sed object at 0x7efc78aa6290>, 'full_continuum_nlr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa5450>, 'disc_escaped': <synthesizer.emissions.sed.Sed object at 0x7efc78aa4ca0>, 'disc_transmitted_nlr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa5510>, 'disc_transmitted_blr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa5d50>, 'nlr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa7640>, 'blr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa4b80>, 'torus': <synthesizer.emissions.sed.Sed object at 0x7efc78aa5570>, 'disc_escaped_isotropic': <synthesizer.emissions.sed.Sed object at 0x7efc78aa6a10>, 'blr_continuum': <synthesizer.emissions.sed.Sed object at 0x7efc78aa41c0>, 'disc_transmitted_nlr_isotropic': <synthesizer.emissions.sed.Sed object at 0x7efc78aa7220>, 'disc_transmitted_blr_isotropic': <synthesizer.emissions.sed.Sed object at 0x7efc78aa4eb0>, 'nlr_continuum': <synthesizer.emissions.sed.Sed object at 0x7efc78aa7dc0>, 'disc_transmitted_weighted_combination': <synthesizer.emissions.sed.Sed object at 0x7efc78a672e0>, 'line_regions': <synthesizer.emissions.sed.Sed object at 0x7efc78a67310>, 'disc_averaged_without_torus': <synthesizer.emissions.sed.Sed object at 0x7efc78a674f0>, 'disc_transmitted': <synthesizer.emissions.sed.Sed object at 0x7efc78a67a60>, 'disc_averaged': <synthesizer.emissions.sed.Sed object at 0x7efc78aa6ce0>, 'disc': <synthesizer.emissions.sed.Sed object at 0x7efc788d1fc0>, 'intrinsic': <synthesizer.emissions.sed.Sed object at 0x7efc788d1ea0>, 'attenuated': <synthesizer.emissions.sed.Sed object at 0x7efc78aa6f80>}
{'disc_incident_masked': <synthesizer.emissions.sed.Sed object at 0x7efc78aa7010>, 'disc_transmitted_nlr_full': <synthesizer.emissions.sed.Sed object at 0x7efc78aa40d0>, 'disc_transmitted_blr_full': <synthesizer.emissions.sed.Sed object at 0x7efc78aa4790>, 'full_reprocessed_nlr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa64d0>, 'full_reprocessed_blr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa6fe0>, 'disc_incident_isotropic': <synthesizer.emissions.sed.Sed object at 0x7efc78aa4c70>, 'full_continuum_blr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa5fc0>, 'disc_transmitted_nlr_isotropic_full': <synthesizer.emissions.sed.Sed object at 0x7efc78aa6200>, 'disc_transmitted_blr_isotropic_full': <synthesizer.emissions.sed.Sed object at 0x7efc78aa5240>, 'disc_incident': <synthesizer.emissions.sed.Sed object at 0x7efc7bb5ffa0>, 'full_continuum_nlr': <synthesizer.emissions.sed.Sed object at 0x7efc7d673670>, 'disc_escaped': <synthesizer.emissions.sed.Sed object at 0x7efc7bb5fdf0>, 'disc_transmitted_nlr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa4ca0>, 'disc_transmitted_blr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa5510>, 'nlr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa5d50>, 'blr': <synthesizer.emissions.sed.Sed object at 0x7efc78aa7640>, 'torus': <synthesizer.emissions.sed.Sed object at 0x7efc78aa4b80>, 'disc_escaped_isotropic': <synthesizer.emissions.sed.Sed object at 0x7efc78aa5570>, 'blr_continuum': <synthesizer.emissions.sed.Sed object at 0x7efc78aa6a10>, 'disc_transmitted_nlr_isotropic': <synthesizer.emissions.sed.Sed object at 0x7efc78aa41c0>, 'disc_transmitted_blr_isotropic': <synthesizer.emissions.sed.Sed object at 0x7efc78aa7220>, 'nlr_continuum': <synthesizer.emissions.sed.Sed object at 0x7efc78aa4eb0>, 'disc_transmitted_weighted_combination': <synthesizer.emissions.sed.Sed object at 0x7efc78aa7dc0>, 'line_regions': <synthesizer.emissions.sed.Sed object at 0x7efc78a672e0>, 'disc_averaged_without_torus': <synthesizer.emissions.sed.Sed object at 0x7efc78a67310>, 'disc_transmitted': <synthesizer.emissions.sed.Sed object at 0x7efc78a674f0>, 'disc_averaged': <synthesizer.emissions.sed.Sed object at 0x7efc78a67a60>, 'disc': <synthesizer.emissions.sed.Sed object at 0x7efc78a67430>, 'intrinsic': <synthesizer.emissions.sed.Sed object at 0x7efc78a67bb0>, 'attenuated': <synthesizer.emissions.sed.Sed object at 0x7efc78aa6ce0>}
Printing Used Parameters¶
During spectra generation, emission models cache the parameters they extract and use from the emitter. These cached parameters can be printed in a nicely formatted table to inspect which values were actually used by each model.
[13]:
# Print the cached parameters used by the models
blackholes.print_used_parameters()
+--------------------------------------------------------------------------------------------+
| MODEL: DISC_INCIDENT_MASKED |
+-------------------------------------+------------------------------------------------------+
| Attribute | Value |
+-------------------------------------+------------------------------------------------------+
| cosine_inclination | 1.00 |
+-------------------------------------+------------------------------------------------------+
| cosine_inclinations | 1.00 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameter | 0.10 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameters | 0.10 |
+-------------------------------------+------------------------------------------------------+
| extract | 'incident' |
+-------------------------------------+------------------------------------------------------+
| emitter | 'blackhole' |
+-------------------------------------+------------------------------------------------------+
| masks | 'torus_edgeon_cond < 90 degree' |
+-------------------------------------+------------------------------------------------------+
| inclination | 0.0 degree |
+-------------------------------------+------------------------------------------------------+
| theta_torus | 10 degree |
+-------------------------------------+------------------------------------------------------+
| torus_edgeon_cond | 10.0 degree |
+-------------------------------------+------------------------------------------------------+
| masses (4,) | 5.53e+07 Msun -> 9.18e+08 Msun (Mean: 3.98e+08 Msun) |
+-------------------------------------+------------------------------------------------------+
| log10masses (4,) | 7.74e+00 -> 8.96e+00 (Mean: 8.36e+00) |
+-------------------------------------+------------------------------------------------------+
| accretion_rates_eddington (4,) | 5.35e-04 -> 7.28e-01 (Mean: 2.82e-01) |
+-------------------------------------+------------------------------------------------------+
| log10accretion_rates_eddington (4,) | -3.27e+00 -> -1.38e-01 (Mean: -1.24e+00) |
+-------------------------------------+------------------------------------------------------+
| metallicities (4,) | 1.00e-02 -> 1.00e-02 (Mean: 1.00e-02) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_density | 10000000000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_densities | 10000000000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| bolometric_luminosities (4,) | 1.61e+10 Lsun -> 1.22e+13 Lsun (Mean: 3.36e+12 Lsun) |
+-------------------------------------+------------------------------------------------------+
+--------------------------------------------------------------------------------------------+
| MODEL: DISC_TRANSMITTED_NLR_FULL |
+-------------------------------------+------------------------------------------------------+
| Attribute | Value |
+-------------------------------------+------------------------------------------------------+
| cosine_inclination | 1.00 |
+-------------------------------------+------------------------------------------------------+
| cosine_inclinations | 1.00 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameter | 0.01 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameters | 0.01 |
+-------------------------------------+------------------------------------------------------+
| extract | 'transmitted' |
+-------------------------------------+------------------------------------------------------+
| emitter | 'blackhole' |
+-------------------------------------+------------------------------------------------------+
| masks | 'torus_edgeon_cond < 90 degree' |
+-------------------------------------+------------------------------------------------------+
| inclination | 0.0 degree |
+-------------------------------------+------------------------------------------------------+
| theta_torus | 10 degree |
+-------------------------------------+------------------------------------------------------+
| torus_edgeon_cond | 10.0 degree |
+-------------------------------------+------------------------------------------------------+
| log10masses (4,) | 7.74e+00 -> 8.96e+00 (Mean: 8.36e+00) |
+-------------------------------------+------------------------------------------------------+
| log10accretion_rates_eddington (4,) | -3.27e+00 -> -1.38e-01 (Mean: -1.24e+00) |
+-------------------------------------+------------------------------------------------------+
| metallicities (4,) | 1.00e-02 -> 1.00e-02 (Mean: 1.00e-02) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_density | 10000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_densities | 10000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| bolometric_luminosities (4,) | 1.61e+10 Lsun -> 1.22e+13 Lsun (Mean: 3.36e+12 Lsun) |
+-------------------------------------+------------------------------------------------------+
+--------------------------------------------------------------------------------------------+
| MODEL: DISC_TRANSMITTED_BLR_FULL |
+-------------------------------------+------------------------------------------------------+
| Attribute | Value |
+-------------------------------------+------------------------------------------------------+
| cosine_inclination | 1.00 |
+-------------------------------------+------------------------------------------------------+
| cosine_inclinations | 1.00 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameter | 0.10 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameters | 0.10 |
+-------------------------------------+------------------------------------------------------+
| extract | 'transmitted' |
+-------------------------------------+------------------------------------------------------+
| emitter | 'blackhole' |
+-------------------------------------+------------------------------------------------------+
| masks | 'torus_edgeon_cond < 90 degree' |
+-------------------------------------+------------------------------------------------------+
| inclination | 0.0 degree |
+-------------------------------------+------------------------------------------------------+
| theta_torus | 10 degree |
+-------------------------------------+------------------------------------------------------+
| torus_edgeon_cond | 10.0 degree |
+-------------------------------------+------------------------------------------------------+
| log10masses (4,) | 7.74e+00 -> 8.96e+00 (Mean: 8.36e+00) |
+-------------------------------------+------------------------------------------------------+
| log10accretion_rates_eddington (4,) | -3.27e+00 -> -1.38e-01 (Mean: -1.24e+00) |
+-------------------------------------+------------------------------------------------------+
| metallicities (4,) | 1.00e-02 -> 1.00e-02 (Mean: 1.00e-02) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_density | 10000000000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_densities | 10000000000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| bolometric_luminosities (4,) | 1.61e+10 Lsun -> 1.22e+13 Lsun (Mean: 3.36e+12 Lsun) |
+-------------------------------------+------------------------------------------------------+
+--------------------------------------------------------------------------------------------+
| MODEL: FULL_REPROCESSED_NLR |
+-------------------------------------+------------------------------------------------------+
| Attribute | Value |
+-------------------------------------+------------------------------------------------------+
| cosine_inclination | 0.50 |
+-------------------------------------+------------------------------------------------------+
| cosine_inclinations | 0.50 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameter | 0.01 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameters | 0.01 |
+-------------------------------------+------------------------------------------------------+
| extract | 'nebular' |
+-------------------------------------+------------------------------------------------------+
| emitter | 'blackhole' |
+-------------------------------------+------------------------------------------------------+
| log10masses (4,) | 7.74e+00 -> 8.96e+00 (Mean: 8.36e+00) |
+-------------------------------------+------------------------------------------------------+
| log10accretion_rates_eddington (4,) | -3.27e+00 -> -1.38e-01 (Mean: -1.24e+00) |
+-------------------------------------+------------------------------------------------------+
| metallicities (4,) | 1.00e-02 -> 1.00e-02 (Mean: 1.00e-02) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_density | 10000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_densities | 10000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| bolometric_luminosities (4,) | 1.61e+10 Lsun -> 1.22e+13 Lsun (Mean: 3.36e+12 Lsun) |
+-------------------------------------+------------------------------------------------------+
+--------------------------------------------------------------------------------------------+
| MODEL: FULL_REPROCESSED_BLR |
+-------------------------------------+------------------------------------------------------+
| Attribute | Value |
+-------------------------------------+------------------------------------------------------+
| cosine_inclination | 0.50 |
+-------------------------------------+------------------------------------------------------+
| cosine_inclinations | 0.50 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameter | 0.10 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameters | 0.10 |
+-------------------------------------+------------------------------------------------------+
| extract | 'nebular' |
+-------------------------------------+------------------------------------------------------+
| emitter | 'blackhole' |
+-------------------------------------+------------------------------------------------------+
| masks | 'torus_edgeon_cond < 90 degree' |
+-------------------------------------+------------------------------------------------------+
| inclination | 0.0 degree |
+-------------------------------------+------------------------------------------------------+
| theta_torus | 10 degree |
+-------------------------------------+------------------------------------------------------+
| torus_edgeon_cond | 10.0 degree |
+-------------------------------------+------------------------------------------------------+
| log10masses (4,) | 7.74e+00 -> 8.96e+00 (Mean: 8.36e+00) |
+-------------------------------------+------------------------------------------------------+
| log10accretion_rates_eddington (4,) | -3.27e+00 -> -1.38e-01 (Mean: -1.24e+00) |
+-------------------------------------+------------------------------------------------------+
| metallicities (4,) | 1.00e-02 -> 1.00e-02 (Mean: 1.00e-02) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_density | 10000000000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_densities | 10000000000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| bolometric_luminosities (4,) | 1.61e+10 Lsun -> 1.22e+13 Lsun (Mean: 3.36e+12 Lsun) |
+-------------------------------------+------------------------------------------------------+
+--------------------------------------------------------------------------------------------+
| MODEL: DISC_INCIDENT_ISOTROPIC |
+-------------------------------------+------------------------------------------------------+
| Attribute | Value |
+-------------------------------------+------------------------------------------------------+
| cosine_inclination | 0.50 |
+-------------------------------------+------------------------------------------------------+
| cosine_inclinations | 0.50 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameter | 0.10 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameters | 0.10 |
+-------------------------------------+------------------------------------------------------+
| extract | 'incident' |
+-------------------------------------+------------------------------------------------------+
| emitter | 'blackhole' |
+-------------------------------------+------------------------------------------------------+
| log10masses (4,) | 7.74e+00 -> 8.96e+00 (Mean: 8.36e+00) |
+-------------------------------------+------------------------------------------------------+
| log10accretion_rates_eddington (4,) | -3.27e+00 -> -1.38e-01 (Mean: -1.24e+00) |
+-------------------------------------+------------------------------------------------------+
| metallicities (4,) | 1.00e-02 -> 1.00e-02 (Mean: 1.00e-02) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_density | 10000000000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_densities | 10000000000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| bolometric_luminosities (4,) | 1.61e+10 Lsun -> 1.22e+13 Lsun (Mean: 3.36e+12 Lsun) |
+-------------------------------------+------------------------------------------------------+
+--------------------------------------------------------------------------------------------+
| MODEL: FULL_CONTINUUM_BLR |
+-------------------------------------+------------------------------------------------------+
| Attribute | Value |
+-------------------------------------+------------------------------------------------------+
| cosine_inclination | 0.50 |
+-------------------------------------+------------------------------------------------------+
| cosine_inclinations | 0.50 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameter | 0.10 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameters | 0.10 |
+-------------------------------------+------------------------------------------------------+
| extract | 'nebular_continuum' |
+-------------------------------------+------------------------------------------------------+
| emitter | 'blackhole' |
+-------------------------------------+------------------------------------------------------+
| masks | 'torus_edgeon_cond < 90 degree' |
+-------------------------------------+------------------------------------------------------+
| inclination | 0.0 degree |
+-------------------------------------+------------------------------------------------------+
| theta_torus | 10 degree |
+-------------------------------------+------------------------------------------------------+
| torus_edgeon_cond | 10.0 degree |
+-------------------------------------+------------------------------------------------------+
| log10masses (4,) | 7.74e+00 -> 8.96e+00 (Mean: 8.36e+00) |
+-------------------------------------+------------------------------------------------------+
| log10accretion_rates_eddington (4,) | -3.27e+00 -> -1.38e-01 (Mean: -1.24e+00) |
+-------------------------------------+------------------------------------------------------+
| metallicities (4,) | 1.00e-02 -> 1.00e-02 (Mean: 1.00e-02) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_density | 10000000000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_densities | 10000000000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| bolometric_luminosities (4,) | 1.61e+10 Lsun -> 1.22e+13 Lsun (Mean: 3.36e+12 Lsun) |
+-------------------------------------+------------------------------------------------------+
+--------------------------------------------------------------------------------------------+
| MODEL: DISC_TRANSMITTED_NLR_ISOTROPIC_FULL |
+-------------------------------------+------------------------------------------------------+
| Attribute | Value |
+-------------------------------------+------------------------------------------------------+
| cosine_inclination | 0.50 |
+-------------------------------------+------------------------------------------------------+
| cosine_inclinations | 0.50 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameter | 0.01 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameters | 0.01 |
+-------------------------------------+------------------------------------------------------+
| extract | 'transmitted' |
+-------------------------------------+------------------------------------------------------+
| emitter | 'blackhole' |
+-------------------------------------+------------------------------------------------------+
| log10masses (4,) | 7.74e+00 -> 8.96e+00 (Mean: 8.36e+00) |
+-------------------------------------+------------------------------------------------------+
| log10accretion_rates_eddington (4,) | -3.27e+00 -> -1.38e-01 (Mean: -1.24e+00) |
+-------------------------------------+------------------------------------------------------+
| metallicities (4,) | 1.00e-02 -> 1.00e-02 (Mean: 1.00e-02) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_density | 10000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_densities | 10000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| bolometric_luminosities (4,) | 1.61e+10 Lsun -> 1.22e+13 Lsun (Mean: 3.36e+12 Lsun) |
+-------------------------------------+------------------------------------------------------+
+--------------------------------------------------------------------------------------------+
| MODEL: DISC_TRANSMITTED_BLR_ISOTROPIC_FULL |
+-------------------------------------+------------------------------------------------------+
| Attribute | Value |
+-------------------------------------+------------------------------------------------------+
| cosine_inclination | 0.50 |
+-------------------------------------+------------------------------------------------------+
| cosine_inclinations | 0.50 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameter | 0.10 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameters | 0.10 |
+-------------------------------------+------------------------------------------------------+
| extract | 'transmitted' |
+-------------------------------------+------------------------------------------------------+
| emitter | 'blackhole' |
+-------------------------------------+------------------------------------------------------+
| log10masses (4,) | 7.74e+00 -> 8.96e+00 (Mean: 8.36e+00) |
+-------------------------------------+------------------------------------------------------+
| log10accretion_rates_eddington (4,) | -3.27e+00 -> -1.38e-01 (Mean: -1.24e+00) |
+-------------------------------------+------------------------------------------------------+
| metallicities (4,) | 1.00e-02 -> 1.00e-02 (Mean: 1.00e-02) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_density | 10000000000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_densities | 10000000000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| bolometric_luminosities (4,) | 1.61e+10 Lsun -> 1.22e+13 Lsun (Mean: 3.36e+12 Lsun) |
+-------------------------------------+------------------------------------------------------+
+--------------------------------------------------------------------------------------------+
| MODEL: DISC_INCIDENT |
+-------------------------------------+------------------------------------------------------+
| Attribute | Value |
+-------------------------------------+------------------------------------------------------+
| cosine_inclination | 1.00 |
+-------------------------------------+------------------------------------------------------+
| cosine_inclinations | 1.00 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameter | 0.10 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameters | 0.10 |
+-------------------------------------+------------------------------------------------------+
| extract | 'incident' |
+-------------------------------------+------------------------------------------------------+
| emitter | 'blackhole' |
+-------------------------------------+------------------------------------------------------+
| log10masses (4,) | 7.74e+00 -> 8.96e+00 (Mean: 8.36e+00) |
+-------------------------------------+------------------------------------------------------+
| log10accretion_rates_eddington (4,) | -3.27e+00 -> -1.38e-01 (Mean: -1.24e+00) |
+-------------------------------------+------------------------------------------------------+
| metallicities (4,) | 1.00e-02 -> 1.00e-02 (Mean: 1.00e-02) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_density | 10000000000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_densities | 10000000000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| bolometric_luminosities (4,) | 1.61e+10 Lsun -> 1.22e+13 Lsun (Mean: 3.36e+12 Lsun) |
+-------------------------------------+------------------------------------------------------+
+--------------------------------------------------------------------------------------------+
| MODEL: FULL_CONTINUUM_NLR |
+-------------------------------------+------------------------------------------------------+
| Attribute | Value |
+-------------------------------------+------------------------------------------------------+
| cosine_inclination | 0.50 |
+-------------------------------------+------------------------------------------------------+
| cosine_inclinations | 0.50 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameter | 0.01 |
+-------------------------------------+------------------------------------------------------+
| ionisation_parameters | 0.01 |
+-------------------------------------+------------------------------------------------------+
| extract | 'nebular_continuum' |
+-------------------------------------+------------------------------------------------------+
| emitter | 'blackhole' |
+-------------------------------------+------------------------------------------------------+
| log10masses (4,) | 7.74e+00 -> 8.96e+00 (Mean: 8.36e+00) |
+-------------------------------------+------------------------------------------------------+
| log10accretion_rates_eddington (4,) | -3.27e+00 -> -1.38e-01 (Mean: -1.24e+00) |
+-------------------------------------+------------------------------------------------------+
| metallicities (4,) | 1.00e-02 -> 1.00e-02 (Mean: 1.00e-02) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_density | 10000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| hydrogen_densities | 10000.0 cm**(-3) |
+-------------------------------------+------------------------------------------------------+
| bolometric_luminosities (4,) | 1.61e+10 Lsun -> 1.22e+13 Lsun (Mean: 3.36e+12 Lsun) |
+-------------------------------------+------------------------------------------------------+
+-----------------------------------------------------------------------------------------------------+
| MODEL: DISC_ESCAPED |
+------------------------------+----------------------------------------------------------------------+
| Attribute | Value |
+------------------------------+----------------------------------------------------------------------+
| transmission_fraction_escape | 0.80 |
+------------------------------+----------------------------------------------------------------------+
| apply_to | 'disc_incident_masked' |
+------------------------------+----------------------------------------------------------------------+
| transformer | "CoveringFraction(covering_attrs=('transmission_fraction_escape',))" |
+------------------------------+----------------------------------------------------------------------+
| emitter | 'blackhole' |
+------------------------------+----------------------------------------------------------------------+
+-----------------------------------------------------------------------------------------------+
| MODEL: DISC_TRANSMITTED_NLR |
+---------------------------+-------------------------------------------------------------------+
| Attribute | Value |
+---------------------------+-------------------------------------------------------------------+
| transmission_fraction_nlr | 0.10 |
+---------------------------+-------------------------------------------------------------------+
| apply_to | 'disc_transmitted_nlr_full' |
+---------------------------+-------------------------------------------------------------------+
| transformer | "CoveringFraction(covering_attrs=('transmission_fraction_nlr',))" |
+---------------------------+-------------------------------------------------------------------+
| emitter | 'blackhole' |
+---------------------------+-------------------------------------------------------------------+
+-----------------------------------------------------------------------------------------------+
| MODEL: DISC_TRANSMITTED_BLR |
+---------------------------+-------------------------------------------------------------------+
| Attribute | Value |
+---------------------------+-------------------------------------------------------------------+
| transmission_fraction_blr | 0.10 |
+---------------------------+-------------------------------------------------------------------+
| apply_to | 'disc_transmitted_blr_full' |
+---------------------------+-------------------------------------------------------------------+
| transformer | "CoveringFraction(covering_attrs=('transmission_fraction_blr',))" |
+---------------------------+-------------------------------------------------------------------+
| emitter | 'blackhole' |
+---------------------------+-------------------------------------------------------------------+
+---------------------------------------------------------------------------------------+
| MODEL: NLR |
+-----------------------+---------------------------------------------------------------+
| Attribute | Value |
+-----------------------+---------------------------------------------------------------+
| covering_fraction_nlr | 0.10 |
+-----------------------+---------------------------------------------------------------+
| apply_to | 'full_reprocessed_nlr' |
+-----------------------+---------------------------------------------------------------+
| transformer | "CoveringFraction(covering_attrs=('covering_fraction_nlr',))" |
+-----------------------+---------------------------------------------------------------+
| emitter | 'blackhole' |
+-----------------------+---------------------------------------------------------------+
+---------------------------------------------------------------------------------------+
| MODEL: BLR |
+-----------------------+---------------------------------------------------------------+
| Attribute | Value |
+-----------------------+---------------------------------------------------------------+
| covering_fraction_blr | 0.10 |
+-----------------------+---------------------------------------------------------------+
| apply_to | 'full_reprocessed_blr' |
+-----------------------+---------------------------------------------------------------+
| transformer | "CoveringFraction(covering_attrs=('covering_fraction_blr',))" |
+-----------------------+---------------------------------------------------------------+
| emitter | 'blackhole' |
+-----------------------+---------------------------------------------------------------+
+-----------------------------------------------------------------------------------------------------------------------------------+
| MODEL: TORUS |
+-------------+---------------------------------------------------------------------------------------------------------------------+
| Attribute | Value |
+-------------+---------------------------------------------------------------------------------------------------------------------+
| emissivity | 1.50 |
+-------------+---------------------------------------------------------------------------------------------------------------------+
| generator | 'Greybody(scaler=disc_incident_isotropic, temperature=1000 K, emissivity=1.5, optically_thin=True, lam_0=100.0 μm)' |
+-------------+---------------------------------------------------------------------------------------------------------------------+
| emitter | 'blackhole' |
+-------------+---------------------------------------------------------------------------------------------------------------------+
| temperature | 1000 K |
+-------------+---------------------------------------------------------------------------------------------------------------------+
+---------------------------------------------------------------------------------------------------------------+
| MODEL: DISC_ESCAPED_ISOTROPIC |
+-----------------------+---------------------------------------------------------------------------------------+
| Attribute | Value |
+-----------------------+---------------------------------------------------------------------------------------+
| covering_fraction_blr | 0.10 |
+-----------------------+---------------------------------------------------------------------------------------+
| covering_fraction_nlr | 0.10 |
+-----------------------+---------------------------------------------------------------------------------------+
| apply_to | 'disc_incident_isotropic' |
+-----------------------+---------------------------------------------------------------------------------------+
| transformer | "EscapingFraction(covering_attrs=('covering_fraction_blr', 'covering_fraction_nlr'))" |
+-----------------------+---------------------------------------------------------------------------------------+
| emitter | 'blackhole' |
+-----------------------+---------------------------------------------------------------------------------------+
+---------------------------------------------------------------------------------------+
| MODEL: BLR_CONTINUUM |
+-----------------------+---------------------------------------------------------------+
| Attribute | Value |
+-----------------------+---------------------------------------------------------------+
| covering_fraction_blr | 0.10 |
+-----------------------+---------------------------------------------------------------+
| apply_to | 'full_continuum_blr' |
+-----------------------+---------------------------------------------------------------+
| transformer | "CoveringFraction(covering_attrs=('covering_fraction_blr',))" |
+-----------------------+---------------------------------------------------------------+
| emitter | 'blackhole' |
+-----------------------+---------------------------------------------------------------+
+---------------------------------------------------------------------------------------+
| MODEL: DISC_TRANSMITTED_NLR_ISOTROPIC |
+-----------------------+---------------------------------------------------------------+
| Attribute | Value |
+-----------------------+---------------------------------------------------------------+
| covering_fraction_nlr | 0.10 |
+-----------------------+---------------------------------------------------------------+
| apply_to | 'disc_transmitted_nlr_isotropic_full' |
+-----------------------+---------------------------------------------------------------+
| transformer | "CoveringFraction(covering_attrs=('covering_fraction_nlr',))" |
+-----------------------+---------------------------------------------------------------+
| emitter | 'blackhole' |
+-----------------------+---------------------------------------------------------------+
+---------------------------------------------------------------------------------------+
| MODEL: DISC_TRANSMITTED_BLR_ISOTROPIC |
+-----------------------+---------------------------------------------------------------+
| Attribute | Value |
+-----------------------+---------------------------------------------------------------+
| covering_fraction_blr | 0.10 |
+-----------------------+---------------------------------------------------------------+
| apply_to | 'disc_transmitted_blr_isotropic_full' |
+-----------------------+---------------------------------------------------------------+
| transformer | "CoveringFraction(covering_attrs=('covering_fraction_blr',))" |
+-----------------------+---------------------------------------------------------------+
| emitter | 'blackhole' |
+-----------------------+---------------------------------------------------------------+
+---------------------------------------------------------------------------------------+
| MODEL: NLR_CONTINUUM |
+-----------------------+---------------------------------------------------------------+
| Attribute | Value |
+-----------------------+---------------------------------------------------------------+
| covering_fraction_nlr | 0.10 |
+-----------------------+---------------------------------------------------------------+
| apply_to | 'full_continuum_nlr' |
+-----------------------+---------------------------------------------------------------+
| transformer | "CoveringFraction(covering_attrs=('covering_fraction_nlr',))" |
+-----------------------+---------------------------------------------------------------+
| emitter | 'blackhole' |
+-----------------------+---------------------------------------------------------------+
+------------------------------------------------------------------------+
| MODEL: DISC_TRANSMITTED_WEIGHTED_COMBINATION |
+----------+-------------------------------------------------------------+
| Attribute | Value |
+----------+-------------------------------------------------------------+
| emitter | 'blackhole' |
+----------+-------------------------------------------------------------+
| combine | [disc_escaped, disc_transmitted_nlr, disc_transmitted_blr,] |
+----------+-------------------------------------------------------------+
+------------------------+
| MODEL: LINE_REGIONS |
+----------+-------------+
| Attribute | Value |
+----------+-------------+
| emitter | 'blackhole' |
+----------+-------------+
| combine | [nlr, blr] |
+----------+-------------+
+---------------------------------------------------------------------+
| MODEL: DISC_AVERAGED_WITHOUT_TORUS |
+----------+----------------------------------------------------------+
| Attribute | Value |
+----------+----------------------------------------------------------+
| emitter | 'blackhole' |
+----------+----------------------------------------------------------+
| combine | [disc_escaped_isotropic, disc_transmitted_nlr_isotropic, |
| | disc_transmitted_blr_isotropic, ] |
+----------+----------------------------------------------------------+
+------------------------------------------------------+
| MODEL: DISC_TRANSMITTED |
+----------+-------------------------------------------+
| Attribute | Value |
+----------+-------------------------------------------+
| emitter | 'blackhole' |
+----------+-------------------------------------------+
| combine | [disc_transmitted_weighted_combination, ] |
+----------+-------------------------------------------+
+-------------------------------------------------------------------------+
| MODEL: DISC_AVERAGED |
+----------------+--------------------------------------------------------+
| Attribute | Value |
+----------------+--------------------------------------------------------+
| apply_to | 'disc_averaged_without_torus' |
+----------------+--------------------------------------------------------+
| transformer | "EscapingFraction(covering_attrs=('torus_fraction',))" |
+----------------+--------------------------------------------------------+
| emitter | 'blackhole' |
+----------------+--------------------------------------------------------+
| torus_fraction | 0.1111111111111111 |
+----------------+--------------------------------------------------------+
+---------------------------------+
| MODEL: DISC |
+----------+----------------------+
| Attribute | Value |
+----------+----------------------+
| emitter | 'blackhole' |
+----------+----------------------+
| combine | [disc_transmitted, ] |
+----------+----------------------+
+------------------------------------+
| MODEL: INTRINSIC |
+----------+-------------------------+
| Attribute | Value |
+----------+-------------------------+
| emitter | 'blackhole' |
+----------+-------------------------+
| combine | [disc, nlr, blr, torus] |
+----------+-------------------------+
+--------------------------------------+
| MODEL: ATTENUATED |
+-------------+------------------------+
| Attribute | Value |
+-------------+------------------------+
| tau_v | 0.50 |
+-------------+------------------------+
| slope | -1.00e+00 |
+-------------+------------------------+
| apply_to | 'intrinsic' |
+-------------+------------------------+
| transformer | 'PowerLaw(slope=-1.0)' |
+-------------+------------------------+
| emitter | 'blackhole' |
+-------------+------------------------+